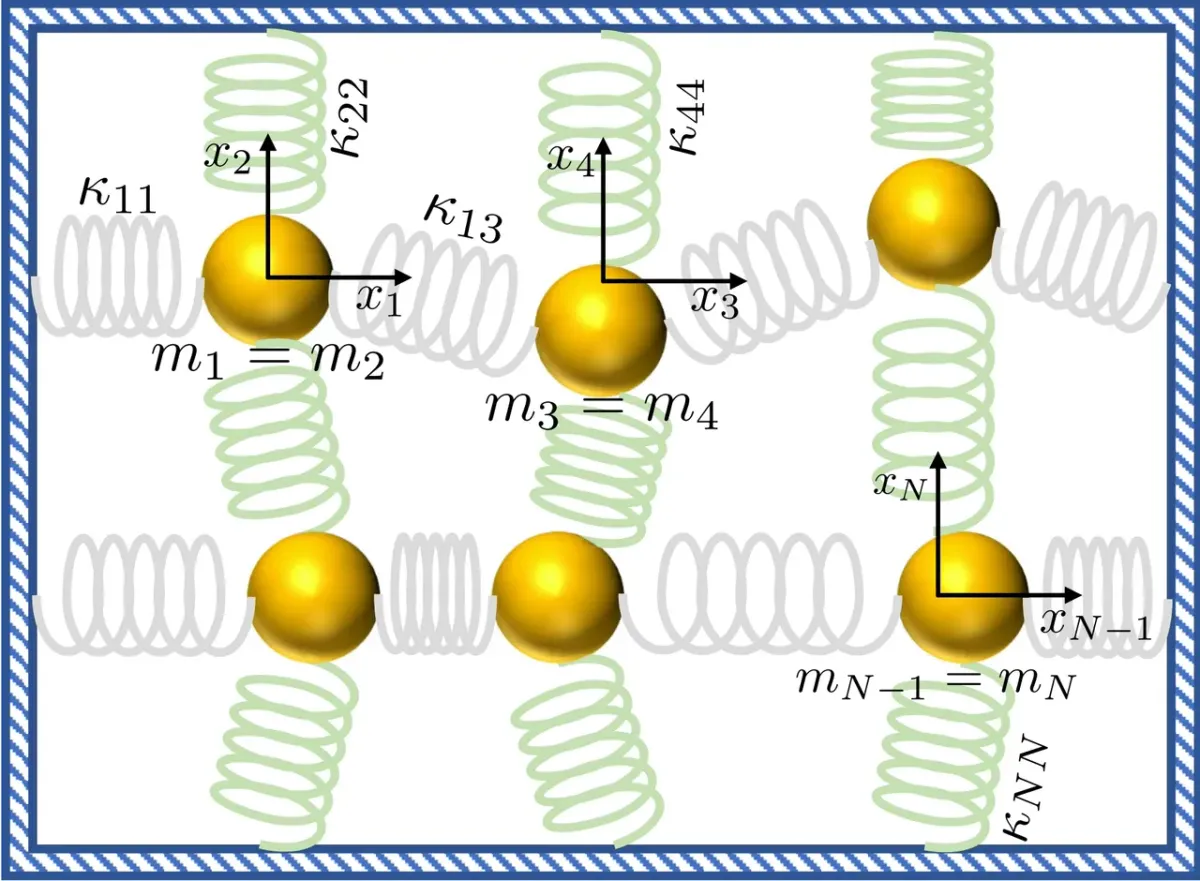
I came across this thought-provoking paper by Babbush et al. (DOI: 10.1103/PhysRevX.13.041041). They demonstrate an intriguing mapping between the dynamics of coupled harmonic oscillators (CHO, classical physics) and the Schrödinger equation. This allows them to solve the system with an exponential speedup using a quantum computer.

However, here's the twist: the mapping is bidirectional. This means that CHO can be used to simulate an arbitrary quantum computer.  If an efficient classical algorithm is ever developed to solve CHO, the exponential advantage offered by quantum computers could be challenged!

This reminds me of a similar scenario with Shor's algorithm for factoring. Is this a tangible sign that the true limits of quantum speedup are one step closer?